Model Select problem

在机器学习的世界里面有非常多的模型（基石这个课暂时只讲了Perceptron Learning Algorithm，Linear Regression,Logistic Regression），各个模型也会有自己不同的特点，有各自长处，也有各自的短处,并且除模型之外，还有其他的附属选择，比如Regularization的类型，或者具体参数的值，比如Gradient Descent里面的步长等，我们知道，现在机器学习的目的就是得到最小化的Eout（也就是测试误差啦），那么现在给你一批数据，然后会出现上述那么多的选择，如果做才能得到最小的Eout呢？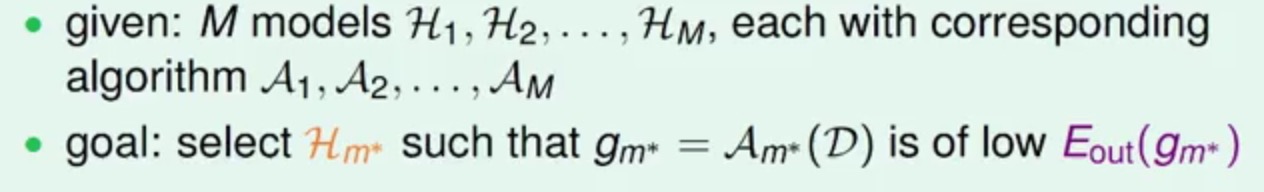

也就是我们要找到一个最好的模型Hm，使得Eout(gm)最小。

看到Eout首先联想到得就是Ein，根据VC Bound可以知道,样本空间存在有限的break point，并且采样的资料量N够多的时候，有一个很大的概率Eout与Ein会很相似，但是又根据VC维中的模型复杂图可以看到，到VC维很高时（模型会很复杂），此时的Ein会很小，但是Eout就会很大了，这样就会出现了BAD Regularization

这里好比一个1126次的多项式的Ein总是能低于1次的多项式-_-，但是其Eout就不一定了

所以说只使用Ein最小化来选择模型并不是很靠谱，因为不能保证得到一个最小的Eout-_-||

现在再来思考一下，假如我们能够得到测试数据的误差Etest,那么Eout会不会与之很相似呢？
关于这个问题Hoeffding不等式又可以出来证明了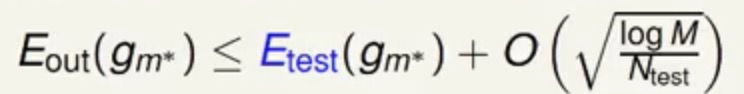
1-2
这里的M表示可以进行模型选择的数量，Ntest表示预测样本的数量，通过上面的不等式可以看到当预测样本足够大，可选模型足够少的时候，Etest和Eout是很就近的。
那么问题来了：关于这个测试样本如何得到？？？这是一个比较大的问题
先来看Ein和Etest这两者的对比

可以发现：

• Ein表示数据比较容易获取，但是可以变相得看做在原有数据集上训练完了 又在该数据库测试了一遍
• Etest测试数据比较难获取，但是一旦得到的测试数据都市无污染的，没有被训练过（也就是没有哎呦）

所以这里又想了一种比较折中的方式

这个折中的方式就是使用现有的训练样本来进行测试，但是这个训练样本是没有被训练过， 这里叫做评估/验证的误差Eval,这中方式的具体做法就是将训练样本分为两部分，一本分用于训练，另一个部分用于测试，通过这种方式就可以有效的选择。

Validation Error

现在假设总资料有N，切出K份来作为验证集，这样关于这个式子就可以有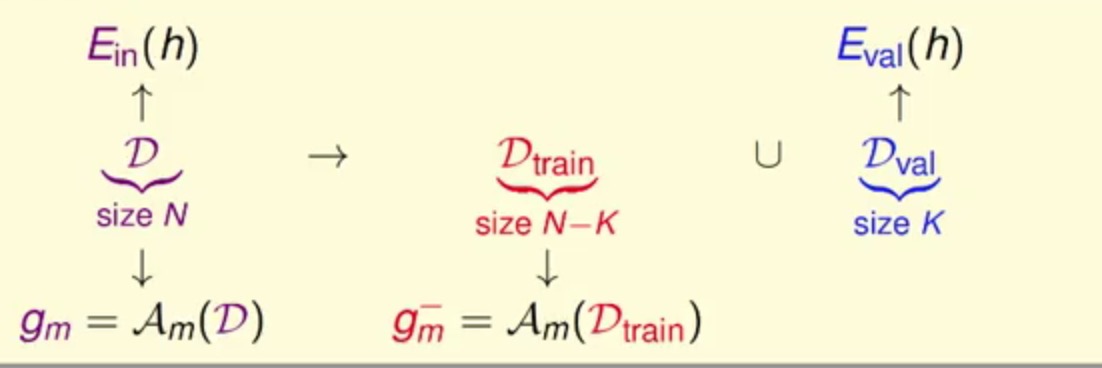

（ps:其中D表示所有的数据集,gm为我们需要的目标函数）
这样的话：

1. Dval表示验证数据集，并且是比较容易得到的
2. 在K合适的情况下Eval与Eout是很接近的
3. Dval数据从训练数据中剥离出来，并且是没有训练过

那么根据上面的式子1-2 可以有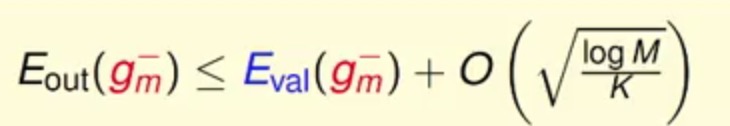

(其中式子里面带减号是为了表示当前训练的数据集并不是全集，而是除去了切出去之后剩余的训练集)

按照上面的思路，我们只需要求Eval的最小化即可
在通过比较最小化的Eval之后得到的模型其实并不是我们需要的最终的模型，因为该模型是在部分数据集上训练得到的，接下来我们还可以将该模型在全集上再次训练出一个新的模型

根据数据集的学习曲线可以了解到 全集训练出模型的Eout将会更加小

所以我们最终产生一个最优模型的学习流程应该是这样的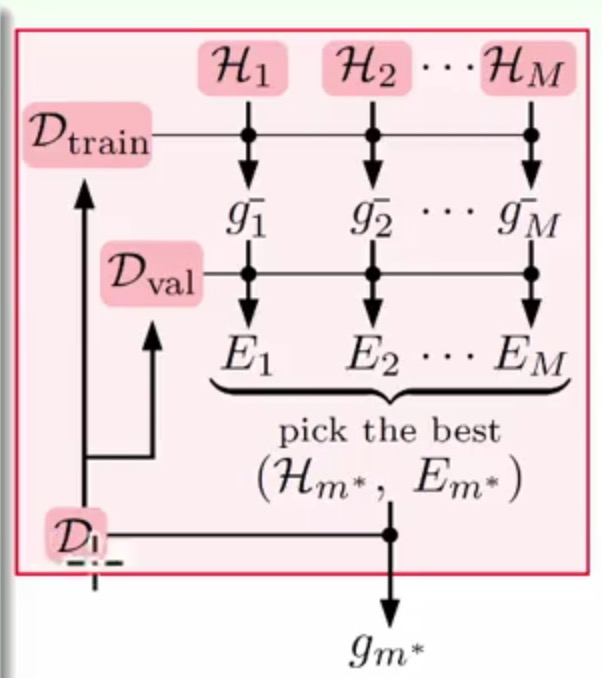

1. 将数据集D分为两份，训练集叫做Dtrain，验证集叫做Dval
2. 将训练集Dtrain输入到各个模型中Hm得到各自的g-m（也就是模型模型训练之后得到的）
3. 将这些训练出来的g-m通过验证集Dval来进行一个验证误差计算Em
4. 将得到Em最小的模型Hm*再次输入到全部数据集中进行一个训练
5. 最终输出全集上的训练得到gm*的结果

这样将上面提到的几个概念连起来之后有

现在来对比一下刚刚提到几种最优模型的选择方法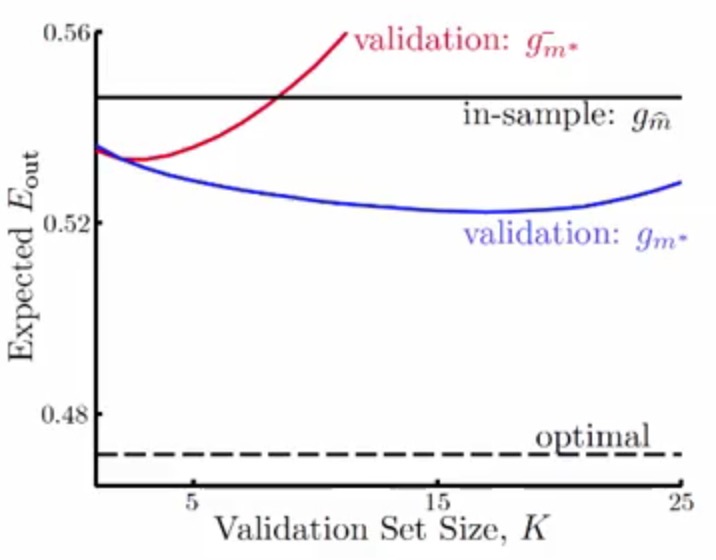
2-6
其中横轴表示验证数据集K的大小，纵轴表示Eout的大小，从图中可以看到

• 黑色的实线表示通过Ein来选择的模型，因为它是在全集上进行的计算，所以总是和验证集的大小没关系，故为一条直线
• 黑色的虚线表示直接在测试集上根据其误差选择的模型，测试集都给你了。。。当然能选择较好的模型，但是这种事情一般都是不现实的。。
• 红色的线表示根据Eval进行模型的选择，但是最终给的模型仍然是在除验证集的训练集上训练得出的
• 蓝色的线表示根据Eval进行模型的选择，但是最终给的模型会重新在全集上进行一次训练
• 可以发现蓝色的线总是优于红色的线，这也说明在全集的训练能将Eout降到更低
• 可以发现蓝色的线也总是低于黑色的实线，这也说明了使用Eval比Ein选择模型更加靠谱
• 还可以发现红色的线会在K到于一定程度之后会高于黑色的实线，这是因为K越大，而总得样本集是一定的，也就是说明能训练的样本就变少了，那么最后训练的g-m的Eval比较大了，也就会导致Eout变大

上图可以总结出使用Eval来选择模型是靠谱的，并且Eval大小也是相当重要的，当然是越小越好

其实使用求Eval最小来选择模型，我们是希望Eval较小的同时可以得到一个较为相似的Eout(g-)，那么我们也可以认为Eout(g-)较小，同时在得到Eout(g-)较小的同时又希望得到相似Eout(g),这才是模型选择的最终目的，但是这两个相似同时成立遂不如人愿啊-_-

1. 看右侧：当K比较大的时候，这样才可以让Eval越准越好，也就是会越接近Eout(g-)

   但是此时的Eout(g-)和Eout(g)就会有较大的偏离的，从图2-6中K>5之后，两者的偏差就会越来越大

2. 看左侧：当K比较小的时候，这样Eout(g-)才是基于较多的训练样本训练出得模型，才能接近Eout(g)，当K=0时，Eout(g-)=Eout(g)

那这个K值的选择可纠结了，该咋选呢？根据林老师的经验建议K=N/5比较合适，其中N为样本总数。

Cross Validation

现在考虑极端情况，当K=1的时候，我们去计算一个Eval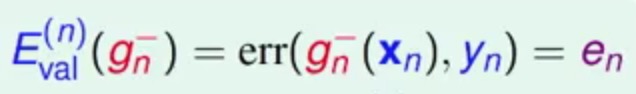

那么这个en会与Eout接近呢？一般一个en不太可能与之接近 -_-|| 想想也是~
那假如我们用N个en来求平均呢？每个en都是用不同的样本进行的校样(假设数据集中的各个样本都把不同)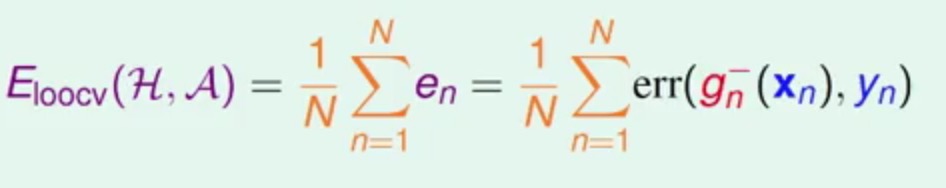

这种方式就是叫做交叉验证（Cross Validation），因为里面同一个样本，有时会作为训练样本，有时会作为测试样本。
在K=1的时候也叫leave one out validation

这张图就可以演示平面上三个点,现有一个一次函数和一个常量来拟合，使用交叉验证来进行选择

那现在咱们只需要能证明Eioocv(H,A)≈Eout(g)即可。

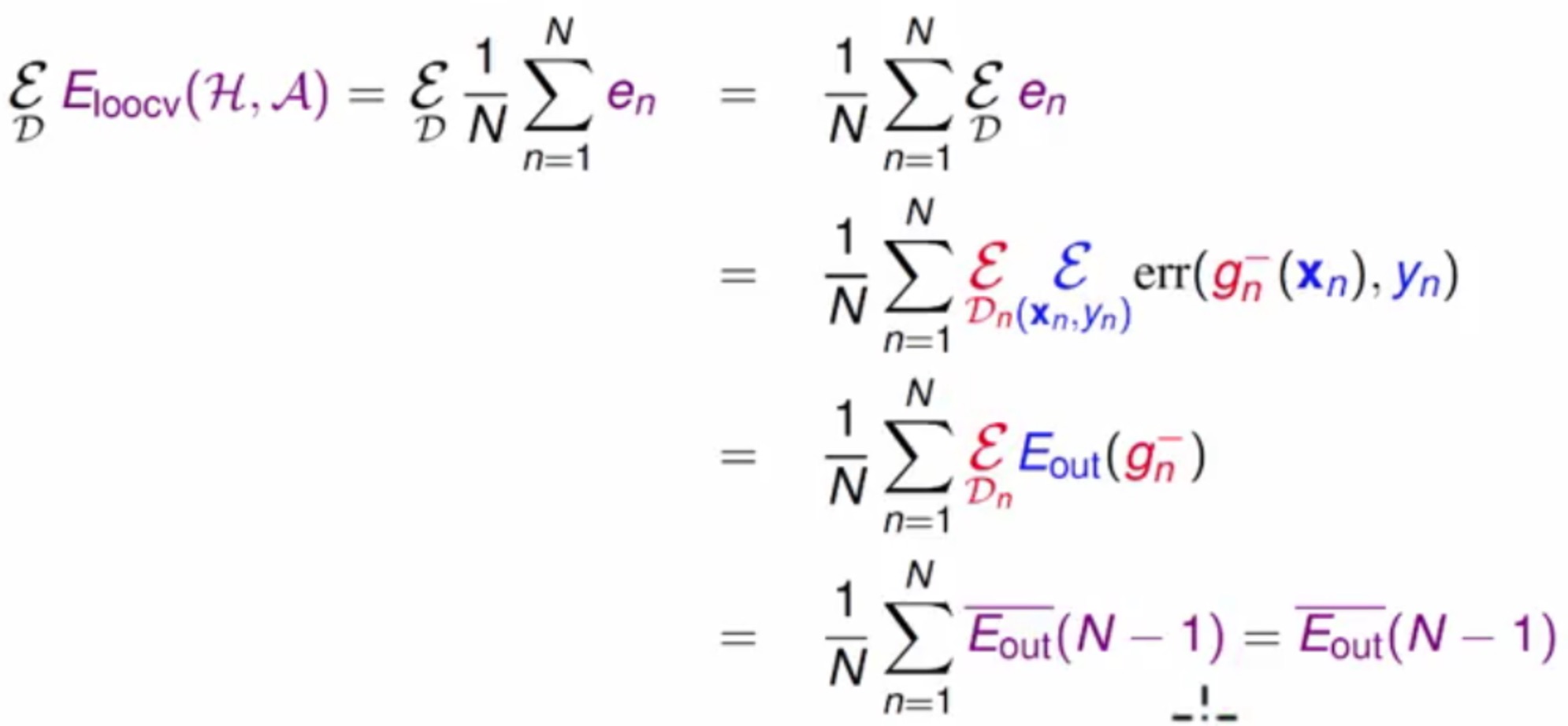
我理解的大致推导的过程是,将整个对Data的期望拆解之后形成Dtrain和Dval，根据Eval推出E-out 再根据对Dtrain上的期望得到Eout(N-1)的平均，再之外围的求和的平均可以抵消，结果就成了在 Eout(N-1)的平均了。ps：当K=1的时候，E-out 和Eout(N-1)很接近,同时Eout(N-1)又会与Eout很接近，这就证明成立了。^_^

Example

到了这里，来看一个实际的例子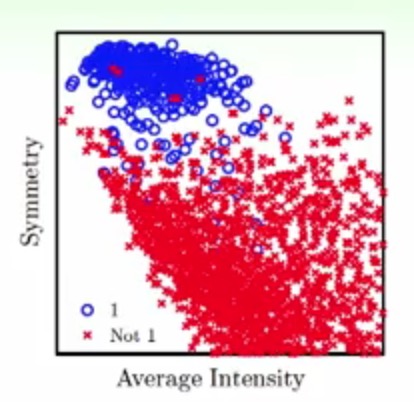

现在需要做一个手写体的识别，来识别是否是1，通过不同的选择方法来进行最优模型的选择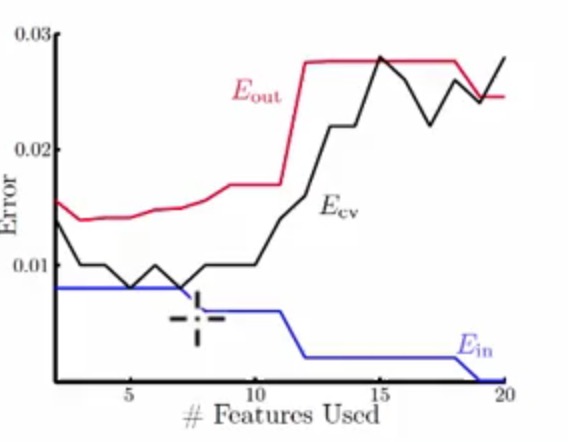

可以发现，随着特征的增加Ein在不断的减少（这点其实很容易理解，与VC维里面的图相似），但是会发现Eout并不是一直的降低，反而特征增加到一定量之后，Eout就上升了
反而来看验证的误差Ecv(cv表示cross validation)，他的曲线几乎与Eout一致，并且在两者最低点的地方也很相似，最终可以分别看到用Ein和Ecv选择出来的模型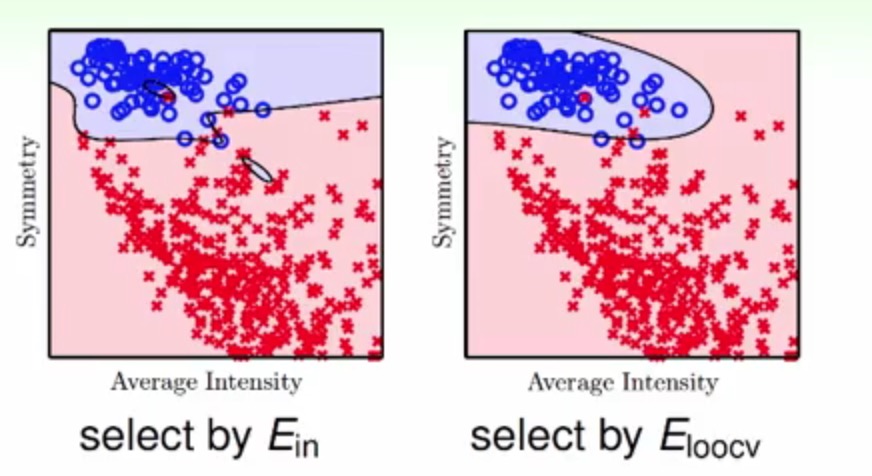

很明显，通过交叉验证选出来的模型更加平滑，也更加不容易过拟合。^_^

V-Fold Cross Validation

上面说的使用leave one out validation的交叉验证来选择模型的效果虽然好，然后难免也存在以下两个主要的问题

1. 计算问题
   可以看到，计算一次Eioocv,都大概需要N次，并且每次训练时的数据量为N-1,那这样整个训练的复杂度野生生的由Ω(N)提升到了Ω(N)2，复杂一些的模型在数据量大一点的情况下整个训练速度已经很难控了，这么一来简直就是灾难。-_-||
2. 稳定性问题
   ps:关于这点现在还是没想通，感觉单个点测试总体平均之后应和v-fold validation一样的-_-，为啥就这个会有这么大的波动。。 来个高手指导下

   所以leave one out validation的交叉验证在实际中并不常用

既然有问题存在，那么如何改善呢？
在leave one out validation中，每个验证的样本只有1个，这个也未免太极端了，现在想想假如将整个样本划分为10分，每一份都轮流做一次验证集,每一轮中其余9份作为训练集，最终将求出来的10个验证集误差Eval求平均

这种方式在效果上其实很类似leave one out validation，但是在计算量上却可以大大的减少，该方式并一定是划分10份，叫做v-fold cross-validation，该v一般取5或者10的效果就已经不错了

虽然这么看来使用Eval已经很错了，但是其实评估一个模型的好坏还是得看Eout，目的不能忘^_^

参考

• 《台湾国立大学-机器学习基石》第十五讲

配图均来自《台湾国立大学-机器学习基石》

---

本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可，我的博客欢迎复制共享，但在同时，希望保留我的署名权kubiCode，并且，不得用于商业用途。如您有任何疑问或者授权方面的协商，请给我留言。